
To do modular addition, you first add the two numbers normally, then divide by the modulus and take the remainder. Thus, the values "wrap around," as you can see below:
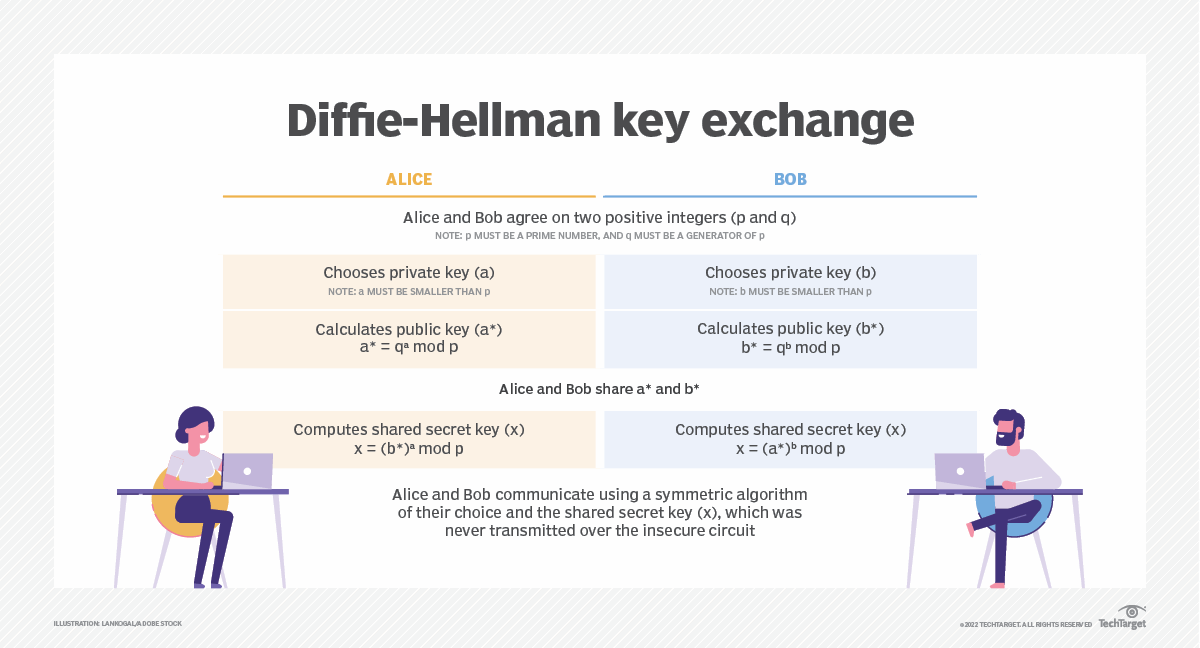
Note that the remainder (when dividing by 7) is always less than 7. In this case, 7 divides into 39 with a remainder of 4. To find, for example, 39 modulo 7, you simply calculate 39/7 (= 5 4/7)Īnd take the remainder. Is basically doing addition (and other operations) not on a line,Īs you usually do, but on a circle - the values "wrap around",Īlways staying less than a fixed number called the modulus. We'll be working a lot with prime numbers, since they have some special properties associated with them. Thus, before we get to the code, we discuss theĪs its only factors 1 and itself (for example, 2, 17, 23, and 127 are prime). Is based on some math that you may not have seen before. Shared secret without anyone else being able to figure out the secret. ThisĪllows two people to publicly exchange information that leads to a Remarkable new way to solve the key-distribution problem. However, in the late 1970's, several people came up with a Initial successful attacks on the Enigma machine. In fact, it was exactly the key distribution problem that led to the

Even the sophisticated Enigma machine required secret keys.

There is a whole network of people (for example, an army) who need toĬommunicate. Trusted courier or an expensive trip), and is wholly impractical if This is quiteĭifficult if they are a long distance apart (it requires either a Must privately and secretly agree on a secret key. One of these is that, somehow, two people who want to use such a system In that the key with which you encipher a plaintext message is the sameĪs the key with which you decipher a ciphertext message.Īs we have discussed from time to time, this leads to several problems. Primes, Modular Arithmetic, and Public Key CryptographyĮvery cipher we have worked with up to this point has been what is Primes, Modular Arithmetic, and Public Key Cryptography Back to Number Theory and Cryptography


 0 kommentar(er)
0 kommentar(er)
